1- Algorithme de recherche d'une occurrence
a- Comprendre le fonctionnement de l'algorithme
Rechercher une occurrence, c'est rechercher dans un tableau si une valeur est présente ou pas.
Soit l'algorithme suivant :
tableau ← [25 , 23, 12, 45, 26, 18, 20]
trouve ← FAUX
nbre ← 45
i ← 0
Tant que i < longueur(tableau) et trouve = FAUX
Si nbre = tableau[ i ] Alors
trouve ←VRAI
FinSi
i ← i + 1
FinPour
Si trouve = VRAI Alors
Ecrire "Le nombre est présent dans le tableau"
Sinon
Ecrire "Le nombre n'est pas présent dans le tableau"tableau est le tableau à parcourir pour chercher une valeur donnée.
trouve est un drapeau qui sera VRAI si la valeur recherchée est trouvée, sinon il sera FAUX
nbre est la valeur à rechercher
Pour comprendre le fonctionnement de cet algorithme, vous allez le faire tourner à la main.
|
Faire tourner à la main un algorithme consiste à se mettre à la place du microprocesseur et de faire fonctionner le programme instruction après instruction. La technique consiste à faire un tableau où les valeurs des variables sont écrites au fur à mesure que le programme se déroule. Dans notre cas, on s'intéresse principalement à ce qui se passe à l'intérieur de la boucle principale. |
Le tableau suivant, illustre la technique de faire tourner à la main :
- Sur la première ligne du tableau :
- l'exécution des instructions des lignes 2, 3 et 4 se trouvent sur les trois premières colonnes.
- arrive en ligne 5 le test de la boucle Tant que (colonne 4 du tableau)
- comme le test est vrai, le traitement se poursuit avec la ligne 6 : est-ce 45=25, ce qui est FAUX
- l'instruction suivante est la ligne 9 : incrémenter i (dernière colonne du tableau)
- Le traitement se poursuit alors à la ligne 5 : A vous de compléter la suite du tableau !

Que se passe-t-il si nbre ← 19 à la place de nbre ← 45 ?
b- Complexité temporelle
L'objectif de déterminer la complexité d'un algorithme est de déterminer sa performance.
|
La complexité d'un algorithme consiste à déterminer la performance de celui-ci. - La performance peut être observée du point de vue du temps, c'est-à-dire en combien de temps le programme arrivera à se terminer. On parle de complexité temporelle. On comprend intuitivement que cela dépend du nombre d'instructions à exécuter. - La performance peut être observée du point de vue de l'occupation de la mémoire lors du traitement. On parle de complexité spatiale. |
Pour simplifier l'approche de travail, on va supposer que chaque instruction prend le même temps pour être exécutée.
L'initialisation du tableau (ligne 1) ne fait pas partie de l'algorithme puisque c'est une donnée de départ.
L'affichage du message (lignes 11 à 14) est indépendant de l'algorithme en soi, parce que cela peut se faire de multiples manières.
Commençons l'analyse de la complexité :
- Il a 3 instructions au début (lignes 2, 3 et 4) qui seront exécutées qu'une fois pour trouver la valeur.
- Pour la boucle ligne 5, tant que la valeur n'est pas trouvée, il y a à chaque tour de boucle 3 instructions à exécuter. Si le tableau à n valeurs, cela fait 3n
- Si la valeur est trouvée (ligne 7) cela fait 1 instruction en plus à faire
Donc la complexité temporelle T = 3 + 3n + 1 soit T = 3n +4, il s'agit d'une fonction linéaire.
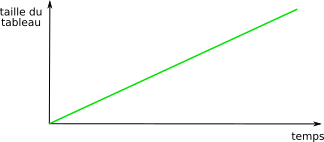 L'écriture de la complexité temporelle T = 3n + 4 peut s'avérer très complexe avec des algorithmes plus sophistiqués.
L'écriture de la complexité temporelle T = 3n + 4 peut s'avérer très complexe avec des algorithmes plus sophistiqués.
Donc, on va imaginer que l'algorithme va traiter des données d'entrée, en tendant leur taille vers l'infini.
Du coup, le 4 peut être enlevé, on obtient une complexité de 3n.
Mais si c'est vraiment tendre vers l'infini, alors 3n est équivalent à n.
On notera donc la complexité d'un algorithme avec la lettre O et pour notre algorithme de recherche d'une occurrence, la complexité sera O = N
Pour d'autres explications, consulter les ressources.
c- Pyhton
Réaliser en python la fonction rechVal(tab,val) et testez-la afin de vérifier le résultat et ensuite coller votre code ci-dessous.
2- Algorithme de recherche d'un extremum
a- Comprendre le fonctionnement de l'algorithme
Soit l'algorithme suivant :
tableau ← [25 , 23, 12, 45, 26, 18, 20]
nbre ← 0
Pour i ← 0 à longueur(tableau)-1
Si nbre<tableau[ i ] Alors
nbre ← tableau[ i ]
FinSi
i Suivant
FinPourEn faisant tourner l'algorithme à la main, quelle est la valeur de nbre une fois l'algorithme terminé ?
b- Déterminer la complexité
Compte tenu des explications de l'activité précédente on ne retiendra pas les 2 premières lignes de l'algorithme.
Combien d'opérations élémentaires faut-il si le tableau ne contenait que 1 valeur ?
Combien d'opérations élémentaires faut-il si le tableau ne contenait que 2 valeurs ?
Combien d'opérations élémentaires faut-il si le tableau ne contenait que 3 valeurs ?
Combien d'opérations élémentaires faut-il si le tableau ne contenait que n valeurs ?
En déduire la complexité de l'algorithme compte tenu des explications de simplification données dans l'activité précédente.
c- Python
Réaliser en python le programme correspondant et lancez-le afin de vérifier le résultat et ensuite coller votre code ci-dessous.
3- Algorithme de calcul de la moyenne
a- Comprendre le fonctionnement de l'algorithme
Soit le tableau tableau ← [25 , 23, 12, 45, 26, 18, 20]
À l'aide d'une boucle Pour ... Suivant ... FinPour proposer l'algorithme qui calcule la moyenne des valeurs du tableau.
Une fois calculé, la valeur de la moyenne sera affichée.
b- Déterminer la complexité
Compte tenu des explications de l'activité précédente, on ne retiendra que les opérations de la boucle de l'algorithme.
Combien d'opérations élémentaires faut-il si le tableau ne contenait que 1 valeur ?
Combien d'opérations élémentaires faut-il si le tableau ne contenait que 2 valeurs ?
Combien d'opérations élémentaires faut-il si le tableau ne contenait que 3 valeurs ?
Combien d'opérations élémentaires faut-il si le tableau ne contenait que n valeurs ?
En déduire la complexité de l'algorithme.
c- Pyhton
Réaliser en python le programme correspondant et lancez-le afin de vérifier le résultat et ensuite coller votre code ci-dessous.
4- CONCLUSION
Dans un parcours séquentiel de tableau la complexité est toujours linéaire :
lorsque le tableau est grand elle est d'ordre N
