La représentation exacte de l'ensemble des réels est impossible : l'ensemble des réels est infini.
La représentation sera donc forcément approximative.
En informatique pour les nombres décimaux, on parle de nombre flottant.
1- Principe de base pour représenter un nombre décimal
1.1 Conversion décimale - binaire
Voici un exemple de représentation avec le nombre : 5,1875.
La partie entière est codée comme nous l'avons déjà vu.
La partie décimale utilise l'algorithme présenté dans le cadre bleu.

Exercice a
Trouvez la représentation binaire de (4,125)10
1.2 Conversion binaire - décimale
Soit le nombre (11,0101)2, retrouvons sa valeur décimale :

Exercices b
- Trouvez la représentation décimale de (101,010)2
- Trouvez la représentation binaire de (0,1)10
Que remarquez-vous ?
- Tester avec Edupython :
>>>0.1+0.2Que remarquez-vous ?
La norme IEEE754 date de 1985 et précise la manière de réprésenter un nombre réel.
Le codage se fait sur un nombre de bits bien défini, avec 2 formats : simple précision et double précision.
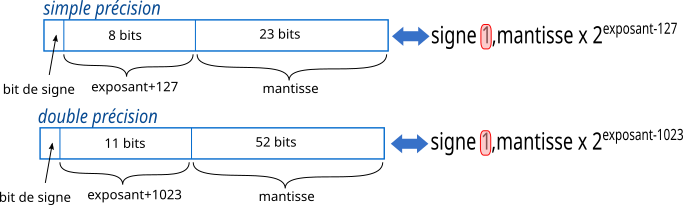
La mantisse représente la partie décimale.
Pourquoi +127 ou +1023 ?
Sur 8 bits il existe 256 valeurs différentes et l'exposant peut être positif ou négatif.
Il a donc été choisi de diviser en 2 afin d'obtenir des exposants positifs et négatif, d'où l'ajout de 127 pour le codage en simple précision.
Par exemple si la valeur de l'exposant est -5, on ne peut pas représenter un nombre négatif, pour n'avoir que des valeurs positives on ajoute systématiquement 127 à la valeur de l'exposant, donc ici -5+127 = 122.
Les valeurs inférieur à 127 représentent donc des exposants négatifs.
Faites l'exercice suivant pour vérifier que vous avez compris.
Pour le codage binaire, vous écrivez les bits par paquets de 4 en les séparant d'un espace.

2.2 Exemple
Afin de comprendre le principe de codage examinons l'exemple suivant avec un codage en simple précision :
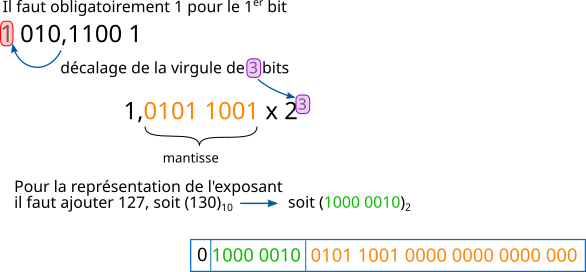
- s'il manque des bits dans la mantisse, on ajoute des 0 à droite,
- s'il manque des bits dans l'exposant, on ajoute des 0 à gauche.
- noter les espaces entre les paquets de 4 bits pour faciliter la lecture du codage.
2.3 Exercices
Déterminez la représentation au format simple précision de (0,25)10 en binaire et en hexadécimal.
Exercice d
Soit le nombre (-0.15625)10, on se propose de le représenter en simple précision avec la norme IEEE754 :
- Trouver dans un premier temps sa représentation en base 2 :
- la partie entière en n'écrivant que les bits significatifs (aucun 0 devant, sauf si le nombre est inférieur à 1) et en mettant un espace tous les 4 bits.
- la partie décimale en mettant un espace tous les 4 bits.
- Trouver ensuite la mantisse et l'exposant de votre nombre afin de respecter l'écriture suivante : 1,1011 0100 x 2+3
- Mettre un espace tous les 4 bits pour la mantisse.
- Trouver le codage en base 2 de l'exposant afin de prendre en compte le signe de l'exposant.
- Mettre un espace tous les 4 bits.
- Compléter les champs de la représentation du nombre avec la norme IEEE754
- la partie de la mantisse que vous devez remplir contient 8 bits.
- S'il manque des 0 sur la mantisse vous devez les ajouter pour obtenir 8 bits.
- Mettre un espace tous les 4 bits.
Exercice e
Tester dans python :
a=1.12e+306
b=1.1e+3
c=a*b
print(a)
print(b)
print(c)Que constatez-vous ?
Quelle est la valeur maximale possible avec la norme IEEE754 ?
Exercice f
Retrouver ci-dessous le codage IEEE754 du nombre -0.03125
![]()
